Задача O. 5. Предсказание ущерба от реализации угроз
Имя входного файла: стандартный ввод
Имя выходного файла: стандартный вывод
Ограничение по времени: 1 с
Ограничение по памяти: 1024 МБ
Имя выходного файла: стандартный вывод
Ограничение по времени: 1 с
Ограничение по памяти: 1024 МБ
Одной из наиболее важных задач в обеспечении безопасности компьютерной системы является обеспечение сбалансированности уровня её защищенности и производительности.
Применение средств защиты информации в корпоративной системе снижает ее производительность по обработке пользовательской информации, так как нужны дополнительные затраты времени на реализацию функций защиты. Т.е. с ростом уровня защищенности снижается производительность и наоборот.
Построение адаптивных саморазвивающихся систем защиты невозможно без интеллектуальных алгоритмов. Одним из недостатков традиционного подхода является задержка во времени между появлением новой атаки и средств защиты от нее. В теории Систем Защиты Информации различают три вида противодействия: опережающее, одновременное и запаздывающее. Запаздывающее противодействие – когда реакция системы защиты начинается к моменту завершения угрозы или после нее. Одновременное противодействие – то, что начинается с появлением угрозы. И, наконец, противодействие, носящее опережающий характер, – когда реакция системы защиты начинается до начала реализации угрозы.
Идеальным вариантом является опережающее противодействие, а для этого необходимо не только наличие методик, позволяющих своевременно обнаружить угрозу безопасности, но и применение алгоритмов, способных выполнить анализ ситуации и выявить предпосылки для такого вторжения.
Пусть в некой системе безопасности реализована методика, позволяющая обнаружить угрозу безопасности. С ее помощью ведется сбор признаков, связанных с возможным проявлением угроз. Чтобы оценить возможный ущерб реализации вторжения, в системе безопасности на основе этих признаков строится регрессионная модель, отражающая зависимость возможного ущерба от значений признаков проявления угрозы.
Задание. В данной задаче вам необходимо восстановить зависимости между значением признака проявления угрозы и возможным ущербом от ее реализации. Такой метод восстановления зависимостей известен под названием линейная регрессия. Согласно методу, необходимо построить прямую, которая делит множество точек так, что сумма квадратов расстояний от этих точек до прямой – минимальна.
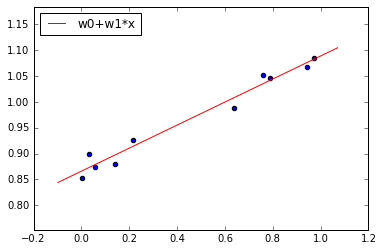

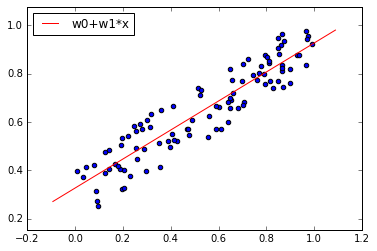
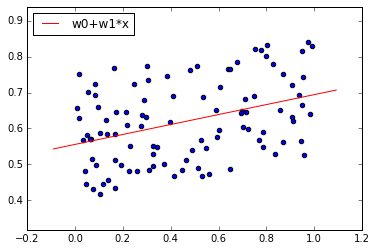
Предсказанный ущерб вычисляется с помощью построенной прямой, на основе признака проявления угрозы (значение на горизонтальной оси)
О линейной регрессии
Итак, линейная регрессия — метод восстановления зависимости между двумя переменными. Его суть в следующем.
Для заданного множества из m пар (x_i, y_i), i=1,..,m, значений требуется построить зависимость между свободной (x_i) и зависимой переменной (y_i).
Считаем, что эта зависимость описывается регрессионной моделью
y_i = f(w,x_i)+\epsilon_i , где \epsilon_i – некоторая случайная величина.
Определим самую простую модель зависимости как y_i = w_0+w_1 x_i+\epsilon_i.
Считаем, что переменные x, y – вещественные числа. Предполагается, что случайная величина распределена нормально с нулевым матожиданием и фиксированной дисперсией \sigma^2_\epsilon, которая не зависит от переменных x, y (хотя это в данной задаче не важно). При таких предположениях параметры w = (w_0, w_1) регрессионной модели вычисляются с помощью метода наименьших квадратов.
Согласно методу наименьших квадратов, искомый вектор параметров w=(w_0, w_1)^T есть решение нормального уравнения w=(A^TA)^{-1}A^Ty, где y — вектор, состоящий из значений зависимой переменной, y=(y_1,...,y_m) .
Матрица имеет вид


Зависимая переменная восстанавливается по полученным весам и заданным значениям свободной переменной y_i^{*}=w_1+w_2 x_i, иначе y^{*}=Aw
Для оценки качества модели используется критерий суммы квадратов регрессионных остатков, SSE — Sum of Squared Errors:
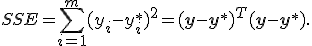
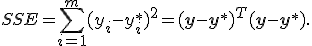
Формат входных данных
В первой строке натуральное число M – количество точек (x, y), 1 \leq M \leq 100000.
Далее идут в M строк, каждая из которых состоит из двух вещественных чисел разделенных пробелами.
Формат выходных данных
В первой строке – значение w_0, округленное до десятых
Во второй строке – значение w_1, округленное до десятых
В третьей строке – значение SSE, округленное до десятых
Пример
| стандартный ввод | стандартный вывод |
|---|---|
| 10 0.6380430609168279 0.9884684868825793 0.9714644905696914 1.084627845903709 0.7588529222137359 1.0526308898451031 0.03063559205401245 0.8999597959939373 0.7868451059875948 1.0466201544281002 0.1404787845534905 0.8791187247740166 0.21461913581247705 0.9266728212944594 0.9416856718651532 1.0680453311757867 0.057676329093018786 0.8738502523915546 0.001532953122964642 0.8524382284168159 | 0.9 0.2 0.0 |